ECUACIONES
DIFERENCIALES
ORDINARIAS
LIBRO DIGITAL INTERACTIVO

ECUACIONES DIFERENCIALES ORDINARIAS
LIBRO DIGITAL INTERACTIVO
Universidad Tecnológica Nacional - República Argentina
Rector: Héctor Aiassa
Vicerrector: Haroldo Avetta
Secretaria Académica: Liliana Cuenca Pletsch
www.utn.edu.ar
EdUTecNe - Editorial de la Universidad Tecnológica Nacional
Coordinador General: Fernado H. Cejas
Directora de Edición: Patricia V. Cejas
Coordinador del Comité Editorial: Jaime Moragues
Área Pre-prensa y Producción: Carlos S. Busqued
Director Colección Energías Renovables, Uso Racional de Energía, Ambiente: Jaime Moragues

Esta obra está bajo licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual. Todos los objetos interactivos y los contenidos de esta obra están protegidos por la Ley de Propiedad Intelectual.

ECUACIONES DIFERENCIALES ORDINARIAS Valeria Iliana Bertossi
edUTecNe
LIBRO DIGITAL INTERACTIVO
Sonia Pompeya Pastorelli
Eva Silvana Casco
Buenos Aires, 2019
Ecuaciones Diferenciales Ordinarias
Libro Digital Interactivo
Valeria Iliana Bertossi, Sonia Pompeya Pastorelli, Eva Silvana Casco
Concepción, diseño y edición: Valeria Iliana Bertossi
Objetos de aprendizaje interactivos: Valeria Iliana Bertossi
Librería turn.js: Emmanuel García
Herramientas de edición: DescartesJS, Geogebra
Asesores de programación en el entorno DescartesJS: Juan Guillermo Rivera Berrío, José Román Galo Sánchez
 Impreso en Argentina – Printed in Argentina
Impreso en Argentina – Printed in Argentina
ISBN 978-987-4998-06-4
Queda hecho el depósito que marca la ley 11.723
© edUTecNe, Año 2019
Sarmiento 440, Piso 6
(C1041AAJ) Buenos Aires, República Argentina
A Lautaro, por su amorosa paciencia;
a Cristian, por su apoyo incondicional;
y a mis queridos alumnos, que sin ellos no hubiera sido posible esta obra.
Valeria
A Humberto Pampiglioni, mi profesor modelo.
A mis alumnos, que me enseñan constantemente
y son mi fuente de inspiración.
A Virginia y Eduardo De Santis, que día a día me enlazan a lo importante.
A Dios, que guía mis elecciones y me regala la dicha de ser docente.
Sonia
A la U.T.N., que me ha formado y ha puesto en mi camino docentes motivadores,
amantes del Cálculo, que me han transmitido
sus conocimientos, su pasión y dedicación a la labor docente.
A mis hijos, Ma. Pilar y Nicolás, y a Sandro por su comprensión
y apoyo permanente en mi labor; y a mi familia, por estar siempre.
A mis alumnos, motivo por el cual no pierdo el entusiasmo de seguir creciendo,
pues sin ellos no tendría sentido mi trabajo.
Eva
SECCIÓN I: Ecuación Diferencial Ordinaria
Lineal de Primer Orden
SECCIÓN II: Ecuación Diferencial Ordinaria
Lineal de Orden Superior
SECCIÓN III: Sistema Lineal de Ecuaciones
Diferenciales Ordinarias con coeficientes constantes
Prólogo
Hoy en día nos encontramos en una sociedad en transformación, con nuevas posibilidades para el acceso al conocimiento y con herramientas que potencian la relación entre los conceptos al momento de aprender. La adaptación de los procesos de enseñanza/aprendizaje a esta sociedad, a sus procesos, a sus nuevas costumbres y requerimientos es un gran desafío que como docentes pretendemos abordar.
La idea de este libro nace a partir de los escritos de la Mg. Ing. Sonia Pastorelli. Y, como en el marco de la cultura del aprendizaje nos encontramos ante la necesidad de brindarle a los jóvenes un nuevo escenario que aproveche las TIC, es así como surge el diseño y programación de un simulador de sistemas dinámicos bidimensionales, DaVinci, como tesis final de la carrera de grado en Ingeniería en Sistemas de Información de la Ing. Valeria Bertossi, que fuera dirigida por la Mg. Ing. Pastorelli. El simulador resultó muy útil a la hora de enseñar y nos motivó, como docentes, a explotar el potencial de las tecnologías emergentes al servicio de diversos propósitos educativos. Por ello nos propusimos un largo camino cuyo
9
producto resultara este libro digital de ecuaciones diferenciales, con la dirección de la Ing. Eva Casco y el apoyo de la UTN, en el que las autoras volcamos todo nuestro conocimiento y experticia.
Este objeto de aprendizaje interactivo combina la multimedia con objetivos didácticos propios y actividades interactivas de aprendizaje para su consecución, pues poseen un gran potencial comunicativo, informacional, colaborativo, interactivo, creativo e innovador.
A través de él esperamos que nuestros alumnos puedan conocer y apropiarse de la realidad desde sus contemporáneos recursos tecnológicos.
10
Índice
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden.17
11
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior.55
2. Ecuación Diferencial Ordinaria Lineal (EDO L) de Orden Superior.57
Teorema 1: Condición suficiente para la unicidad de la solución de una
EDO L.58
Teorema 4: Combinación lineal de soluciones pariculares de una EDO
homogénea. 60
2.3. EDO Lineal de orden superior No Homogénea con coeficientes
constantes (EDO L NH cc).65
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con
coeficientes constantes.83
13
4.2. Punto de equilibrio de un sistema lineal. Estabilidad.111
14
15
SECCIÓN I

SECCIÓN I
Ecuación Diferencial Ordinaria
de Primer Orden
"¿Cómo puede ser que la Matemática,
siendo al fin y al cabo,
un producto del pensamiento humano
independiente de la experiencia,
esté tan admirablemente adaptada
a los objetos de la realidad?"
Albert Einstein
18
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
1. Ecuación Diferencial Ordinaria (EDO) de Primer Orden.
En muchos problemas ingenieriles las relaciones entre variables se establecen en función de razones de cambio. Algunos ejemplos son:

En esta sección se formalizará el concepto y se verán técnicas para resolver algunas de las ecuaciones diferenciales más usadas en ingeniería.
19
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
1.1. Ecuación diferencial (ED).
Una ecuación diferencial es aquélla en la que interviene al menos una derivada o diferencial de una función incógnita. Por ejemplo:

20
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Las ED pueden clasificarse según distintos puntos de vista:
a) Según la cantidad de variables independientes 
La ecuación diferencial ordinaria (EDO) es una ecuación que contiene funciones de una sola variable independiente, y una o más de sus derivadas con respecto a dicha variable. Ejemplos:

La ecuación diferencial parcial (EDP) es una ecuación que contiene funciones de dos o más variables independientes y algunas de sus derivadas con respecto a esas variables. Ejemplo:

21
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
b) Según el orden: El orden de una ED es el mayor orden de derivación que aparece en la ecuación.
Por ejemplo,  es de primer orden mientras que
es de primer orden mientras que  es de orden 3.
es de orden 3.
c) Por el tipo de operación (lineal o no) a la que está afectada la función incógnita Por ejemplo, Estas clasificaciones suelen determinar el método de solución, de allí que es importante reconocerlas. En este libro sólo se tratarán las EDO.

 y
y son lineales, mientras que
son lineales, mientras que  no lo es.
no lo es.22
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Solución y tipos de soluciones.
Una solución de una ecuación diferencial es toda relación entre las variables que no contenga derivadas ni diferenciales y que al remplazarla en la ED, la verifique en un intervalo de las variables, es decir, que la transforme en una identidad.
No todas las ED tienen solución. El tratamiento de la existencia y unicidad de la misma reviste cierta complejidad, por lo que no se abordará dicho problema en este libro. Como cualquier ecuación, las ED pueden o no tener solución, pero si la tienen, no será única.
Por ejemplo, la EDO lineal de primer orden  admite la solución
admite la solución  ya que la verifica. Notar que
ya que la verifica. Notar que  .
.
El lector puede probar que  también lo es.
también lo es.
Hay tres tipos de soluciones para las ED:
23
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Solución general: es de tipo genérico, contiene constantes arbitrarias (tantas como el orden de la ED). Así,  es la solución general de la ecuación de 2º orden
es la solución general de la ecuación de 2º orden  .
.
Solución particular: es cualquier solución que puede obtenerse asignando valores particulares a las constantes arbitrarias. En consecuencia, e
e  son dos soluciones particulares de
son dos soluciones particulares de  . En general, estas soluciones se obtienen con datos adicionales sobre la función buscada, denominados condiciones de frontera o iniciales, tales como
. En general, estas soluciones se obtienen con datos adicionales sobre la función buscada, denominados condiciones de frontera o iniciales, tales como  o
o  .
.
Solución singular: solución de la ED que no puede ser obtenida particularizando la solución general.
 Ejemplo
Ejemplo
Al igual que para resolver una ecuación, no existe método único para resolver una ED, pero sí existen algunos métodos prescriptivos para ciertas clases o familias de EDO. Es más, muchas ED que aparecen naturalmente en otras ciencias no
24
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
han sido solucionadas (aún).
Algunas se resuelven por “inspección” (ensayo y error), lo que consiste en “intuir” una solución, y luego confirmar si dicha solución imaginada verifica la ecuación.
Ecuación de Abel.
El ensayo y error se puede utilizar para resolver la EDO denominada ecuación de Abel:  . Esta ecuación, frecuente en muchas ramas de la ciencia, expresa que la razón de cambio,
. Esta ecuación, frecuente en muchas ramas de la ciencia, expresa que la razón de cambio,  , de una función
, de una función  es proporcional al valor de dicha la función para todo
es proporcional al valor de dicha la función para todo  . No es difícil imaginar una función cuya derivada sea proporcional a sí misma: la función que califica es la exponencial
. No es difícil imaginar una función cuya derivada sea proporcional a sí misma: la función que califica es la exponencial  ya que
ya que  (la derivada es proporcional a la función).
(la derivada es proporcional a la función).
Si además se conoce el valor inicial  de la función buscada (esto es
de la función buscada (esto es  ) puede determinarse la única solución del problema. Así,
) puede determinarse la única solución del problema. Así,  . Luego,
. Luego,  .
.
25
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
 Ejemplo
Ejemplo
En adelante, se desarrollarán métodos que permiten resolver algunas de las EDO que comúnmente se utilizan en ingeniería.
Se separá el estudio en dos partes: las EDO de primer orden y las EDO de orden superior (esto es, orden mayor o igual a 2).
1.2. Algunos métodos para determinar la solución de una EDO de primer orden.
Las EDO de primer orden pueden escribirse genéricamente como  , mientras que la solución general es una familia de curvas cuya ecuación tendrá la forma
, mientras que la solución general es una familia de curvas cuya ecuación tendrá la forma  , siendo
, siendo  una constante arbitraria.
una constante arbitraria.
Se tratarán métodos para solucionar las siguientes EDO de primer orden:
26
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
1.2.1. EDO de primer orden de variables separables
La ecuación  se denomina de variables separables si se puede reescribir de la forma:
se denomina de variables separables si se puede reescribir de la forma:  . O en su forma equivalente:
. O en su forma equivalente:  .
.
Para resolver la ecuación se integra miembro a miembro:  . Si ambas integrales pueden ser resueltas, el problema estará solucionado. Notar que al resolver cada integral aparecerán en ambos miembros una constante de integración, las que se reunirán en una.
. Si ambas integrales pueden ser resueltas, el problema estará solucionado. Notar que al resolver cada integral aparecerán en ambos miembros una constante de integración, las que se reunirán en una.
 Ejemplo
Ejemplo
1.2.2. EDO de primer orden homogénea.
La ecuación  se denomina homogénea si se
se denomina homogénea si se
27
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
puede reescribir de la forma  . Con la sustitución
. Con la sustitución  se la transforma en una EDO de variables separables.
se la transforma en una EDO de variables separables.

Notar que  depende de
depende de  . Derivando m. a m. respecto de
. Derivando m. a m. respecto de  :
:

Reemplazando las ecuaciones anteriores en  :
:

Operando:  .
.
De este modo, la ecuación tiene las variables separadas. Se resuelve como la desarrollada en el  .
.
 Ejemplo
Ejemplo
28
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
1.2.3. EDO Lineal de primer orden.
Es aquélla que puede escribirse de la forma  ,
donde
,
donde  y
y son funciones continuas sobre un intervalo dado. Por ejemplo:
son funciones continuas sobre un intervalo dado. Por ejemplo:  .
.
Para resolverla se utilizará un recurso muy utilizado en la resolución de ecuaciones diferenciales, que es el uso de un factor integrante. Pero para entender mejor la esencia del procedimiento se resolverá, a modo de ejemplo constructivo, la ecuación 
La clave para resolverla será multiplicar m. a m. por la función  (operación válida ya que
(operación válida ya que  ).
).

Si se observa con atención, los dos sumandos del primer miembro se puede expresar como la derivada del producto  ya que
ya que  . Así la ecuación se reescribe
. Así la ecuación se reescribe  .
.
Integrando m. a m. se tiene:
29
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

Usando propiedades de la integral indefinida:


Explicitando la solución general:

Notar que la clave fue transformar el primer miembro en la derivada de un producto (al multiplicar por el factor  ), lo que permitió luego calcular su integral. A ese factor (
), lo que permitió luego calcular su integral. A ese factor ( en este caso) se lo denomina factor integrante.
en este caso) se lo denomina factor integrante.
Se probará ahora que  tiene como factor integrante una función
tiene como factor integrante una función  calculándolo.
calculándolo.
30
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
 multiplicando m. a m. por
multiplicando m. a m. por 

Al igual que en el ejemplo anterior se supone que el primer miembro es la derivada de un producto:
 (*)
(*)
Entonces deberá cumplirse:

Luego,  debe ser tal que convierta en igualdad:
debe ser tal que convierta en igualdad:


31
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Dado que P(x) es continua, se garantiza la existencia de I(x). Luego:

El valor  indica que hay infinitos factores integrantes, pero para resolver la EDO se necesita sólo uno. Por ello se adoptará el más sencillo:
indica que hay infinitos factores integrantes, pero para resolver la EDO se necesita sólo uno. Por ello se adoptará el más sencillo:  . Luego,
. Luego,  . Así, reemplazando en (*):
. Así, reemplazando en (*):

Integrando m.a m.:


Explicitando la solución buscada:

32
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Nuevamente, la existencia de y está garantizada porque P(x) y Q(x) son funciones continuas en un intervalo dado, y, por lo tanto, integrables en él.
Resumiendo:
Dada  ;
;  y
y  funciones continuas sobre un intervalo
funciones continuas sobre un intervalo 

 Ejemplo
Ejemplo
1.2.4. EDO Exacta de primer orden.
Es aquélla que puede llevarse a la forma  ó
ó  , siendo
, siendo  una función con derivadas de segundo orden continuas en una región D de R2.
una función con derivadas de segundo orden continuas en una región D de R2.
33
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Recuerde que y es función de x. La solución de la ecuación puede sospecharse  , dado que si se aplica la regla de la cadena se obtendrá la EDO dada, luego la verifica.
, dado que si se aplica la regla de la cadena se obtendrá la EDO dada, luego la verifica.
La pregunta obligada es cómo advertir que  puede llevarse a
puede llevarse a  Dicho de otra manera, ¿existe la función
Dicho de otra manera, ¿existe la función  tal que
tal que  y
y  ?
?
Recordando el teorema de Clairut

 . Por lo tanto, deberá cumplirse:
. Por lo tanto, deberá cumplirse:  y
y  .
.
Luego, el criterio de exactitud puede expresarse como:
La EDO ;
;  y
y  funciones con derivadas continuas sobre una región D del plano xy, es exacta si y sólo si
funciones con derivadas continuas sobre una región D del plano xy, es exacta si y sólo si  .
.
Si se da dicha condición se buscará entonces la función 
34
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
resolviendo el sistema:

 Ejemplo
Ejemplo
1.2.5. EDO de primer orden transformables en exactas.
Muchas ED se transforman en exactas usando un factor integrante. Se desarrollará ahora un método para concluir si una EDO de primer orden tiene o no un factor integrante del tipo  o
o  que la convierta en una EDO exacta, para la cual ya se desarrolló un método que la soluciona.
que la convierta en una EDO exacta, para la cual ya se desarrolló un método que la soluciona.
Condición de existencia del factor integrante  :
:

Multiplicando m.a.m, por  :
:

Usando el criterio de exactitud:
35
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

Desarrollando las derivadas:

Agrupando los términos que contienen  :
:

Luego,  . Notar que, si existe ese
. Notar que, si existe ese  buscado, el segundo miembro es una función que sólo depende de la variable
buscado, el segundo miembro es una función que sólo depende de la variable  ; luego el primer miembro también deberá serlo, es decir,
; luego el primer miembro también deberá serlo, es decir,  es función de
es función de  (condición de existencia de
(condición de existencia de  ).
).
En ese caso, integrando m. a m.:
36
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

Luego, el factor integrante es:
Condición de existencia del factor integrante  :
:

Multiplicando m. a m. por  :
:

Usando el criterio de exactitud:

Desarrollando las derivadas:

37
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Agrupando los términos que contienen  :
:

Luego,  . Notar que, si existe ese
. Notar que, si existe ese  buscado, el segundo miembro es una función que sólo depende de la variable
buscado, el segundo miembro es una función que sólo depende de la variable  , luego el primer miembro también deberá serlo.
, luego el primer miembro también deberá serlo.
En ese caso, integrando m.a m.:

Luego, el factor integrante es: 
Finalmente puede resumirse:
38
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Dada la EDO  ;
;  y
y  funciones con derivadas continuas sobre una región D del plano xy:
funciones con derivadas continuas sobre una región D del plano xy:
Si  es función sólo de
es función sólo de 
 el factor integrante
el factor integrante  la transforma en exacta.
la transforma en exacta.
Si  es función sólo de
es función sólo de 
 el factor integrante
el factor integrante  la transforma en exacta.
la transforma en exacta.
Este teorema no asegura que todas las EDO de primer orden tengan factor integrante, ni tampoco permite encontrar todos los factores integrantes posibles de la misma. Sólo permite encontrar, suponiendo que los tenga, factores integrantes univariables.
39
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
 Ejemplo
Ejemplo
1.3. Aplicaciones
Hasta aquí se han desarrollado algunos de los métodos más comunes que resuelven EDO de primer orden. Se verán ahora algunas aplicaciones de las mismas.
1.3.1. Trayectorias de flujo. Simulador DaVinci
Simulador DaVinci
Las trayectorias de flujo de un campo vectorial son las seguidas por una partícula cuyo campo de velocidad es el campo vectorial dado. Por consiguiente los vectores del campo vectorial son tangentes a las líneas de flujo.
 Ver ejemplo
Ver ejemplo

40
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
1.3.2. Familias ortogonales.
Una trayectoria ortogonal de una familia de curvas  es otra curva que cruza a cada una de las curvas de la familia de manera ortogonal. La colección de trayectorias ortogonales de una familia forma lo que se denomina familia ortogonal
es otra curva que cruza a cada una de las curvas de la familia de manera ortogonal. La colección de trayectorias ortogonales de una familia forma lo que se denomina familia ortogonal  . Se dice que son familias mutuamente ortogonales. Por cada punto
. Se dice que son familias mutuamente ortogonales. Por cada punto  cuya abscisa pertenezca al dominio pasa una integrante de cada una de ellas. Las rectas tangentes a las mismas forman un ángulo recto. Luego, sus pendientes
cuya abscisa pertenezca al dominio pasa una integrante de cada una de ellas. Las rectas tangentes a las mismas forman un ángulo recto. Luego, sus pendientes  y
y  verifican la relación
verifican la relación  . Entonces
. Entonces  .
Esto permite concluir que conocida la ecuación
.
Esto permite concluir que conocida la ecuación  que representa una familia de curvas, su familia ortogonal estará representada por la ED
que representa una familia de curvas, su familia ortogonal estará representada por la ED  .
.
 Ejemplos
Ejemplos
Las familias ortogonales son muy utilizadas en ingeniería. Por
41
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

Idéntica situación se da en problemas de flujo bidimensionales (como el correspondiente a una presa hidráulica tal cual se muestra en el corte): las líneas de flujo  (trayectoria del agua) son perpendiculares a las líneas equipotenciales (líneas que unen los puntos con igual presión).
(trayectoria del agua) son perpendiculares a las líneas equipotenciales (líneas que unen los puntos con igual presión).
1.3.3. Circuitos eléctricos.
 Ejemplo
Ejemplo
Se deja como ejercicio resolver el caso genérico, fuerza:  ; inductancia
; inductancia  y resistencia
y resistencia  ; esto es,
; esto es,
42
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
la EDO a resolver es:

En este caso se deberá probar que la corriente estará dada por:

43
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
Ejercitación propuesta.
Conceptos básicos, ecuaciones separables y homogéneas.
1- Resuelva la siguiente ecuación diferencial:

2- Resuelva el problema con valor inicial:

 Simulador DaVinci
3- Resuelva el problema con valor inicial
Simulador DaVinci
3- Resuelva el problema con valor inicial  ,
,  Investigue el concepto de campo direccional y grafíquelo junto a la solución usando el simulador DaVinci.
Investigue el concepto de campo direccional y grafíquelo junto a la solución usando el simulador DaVinci.
 .
.
 Simulador DaVinci4- Dibuje el campo direccional de la ecuación diferencial. Después utilícelo para dibujar la curva solución que pase a
Simulador DaVinci4- Dibuje el campo direccional de la ecuación diferencial. Después utilícelo para dibujar la curva solución que pase a
44
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
través del punto dado.

 Simulador DaVinci5- Dada:
Simulador DaVinci5- Dada: 
a) Dibuje el campo direccional.
b) Grafique algunas curvas solución, sin resolver la ecuación diferencial.
c) Resuelva la ecuación diferencial. 
d) Dibuje las soluciones obtenidas en el inciso (c) y compárelas con las gráficas del (b).
6- Diga si la ecuación es homogénea:

7- Resuelva las siguientes ecuaciones diferenciales homogéneas:

45
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

![]() Interactivo de Familias Ortogonales 8- Encuentre las trayectorias ortogonales de la familia de curvas. Dibuje a varios miembros de cada familia:
Interactivo de Familias Ortogonales 8- Encuentre las trayectorias ortogonales de la familia de curvas. Dibuje a varios miembros de cada familia:

9- Sean  y
y  la altura y el volumen de agua que hay dentro de un tanque, en un tiempo
la altura y el volumen de agua que hay dentro de un tanque, en un tiempo  dado. Si el agua se derrama a través de un orificio que está en el fondo del tanque y cuya área es
dado. Si el agua se derrama a través de un orificio que está en el fondo del tanque y cuya área es  , entonces la ley de Torricelli dice que:
, entonces la ley de Torricelli dice que:  , donde
, donde  es la aceleración debida a la gravedad.
es la aceleración debida a la gravedad.
a) Suponga que el tanque es cilíndrico y que tiene una altura de 2 m y un radio de 0,5 m y además que el orificio es circular y con un radio de 0,5 cm. Si tomamos  ,
,
46
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
muestre que  satisface la ecuación diferencial
satisface la ecuación diferencial  .
.
b) Resuelva esta ecuación paradeterminar la altura del agua en función del tiempo  , suponiendo que el tanque está lleno en el tiempo
, suponiendo que el tanque está lleno en el tiempo  .
.
c) ¿Cuánto tiempo pasará para que el tanque se vacíe por completo?

Ecuaciones lineales de primer orden.
1- Determine si la ecuación diferencial es lineal:

2- Resuelva las siguientes ecuaciones diferenciales:

47
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

3- Resuelva el problema con valor inicial:

4- Resolver:

5- La ecuación no lineal  se la denomina ecuación de Bernoulli.
se la denomina ecuación de Bernoulli.
a) Muestre que se transforma en una EDO lineal realizando el cambio de variable  .
.
48
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
b) Use el resultado anterior para resolver y verificar las ecuaciones:

6- En el circuito mostrado en la figura, una batería 
 suministra una voltaje constante de
suministra una voltaje constante de  , la inductancia es de
, la inductancia es de  , la resistencia es de
, la resistencia es de  , y además
, y además  .
.
a) Encuentre  .
.
b) Determine la corriente después de  .
.

7- La figura muestra un circuito que contiene una fuerza electromotriz (fem), un capacitor con una capacitancia  faradios
faradios  , y un resistor con una resistencia de
, y un resistor con una resistencia de  ohms
ohms  . La caída de tensión a través del capacitor es
. La caída de tensión a través del capacitor es  , donde
, donde  es
es
49
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
la carga (en Coulomb).
La segunda ley de Kirchoff establece  . Pero
. Pero  , así que se tiene
, así que se tiene  .
.
Suponga que la resistencia es de  , la capacitancia es de
, la capacitancia es de  , que una batería suministra un voltaje constante de
, que una batería suministra un voltaje constante de  y que la carga inicial es de
y que la carga inicial es de  . Determine la carga y la corriente en el tiempo
. Determine la carga y la corriente en el tiempo  .
.

8- Los psicólogos interesados en la teoría del aprendizaje estudian las curvas de aprendizaje. Una curva de aprendizaje es la gráfica de una función  , el desempeño de alguien que está aprendiendo alguna habilidad, como una función del tiempo
, el desempeño de alguien que está aprendiendo alguna habilidad, como una función del tiempo  de capacitación. La derivada
de capacitación. La derivada  , representa la razón con la cual el desempeño mejora. Si
, representa la razón con la cual el desempeño mejora. Si  es el nivel máximo de desempeño que puede tener un aprendiz, resulta razonable suponer que
es el nivel máximo de desempeño que puede tener un aprendiz, resulta razonable suponer que  es proporcional a
es proporcional a  . (Al principio, el aprendizaje es rápido. Después, conforme el
. (Al principio, el aprendizaje es rápido. Después, conforme el
50
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden
desempeño aumenta y se aproxima a su valor máximo, la razón de aprendizaje disminuye). En consecuencia:  . Donde
. Donde  es una constante positiva. Resuelva esta ecuación diferencial lineal y dibuje la curva de aprendizaje.
es una constante positiva. Resuelva esta ecuación diferencial lineal y dibuje la curva de aprendizaje.

9- Un objeto con una masa  se lanza desde su estado de reposo y suponemos que la resistencia del aire es proporcional a la velocidad del objeto. Si
se lanza desde su estado de reposo y suponemos que la resistencia del aire es proporcional a la velocidad del objeto. Si  es la distancia recorrida después de
es la distancia recorrida después de  segundos, entonces la velocidad es
segundos, entonces la velocidad es  y la aceleración es
y la aceleración es  . Si
. Si  es la aceleración debida a la gravedad, entonces la fuerza de atracción sobre un objeto es
es la aceleración debida a la gravedad, entonces la fuerza de atracción sobre un objeto es  , donde
, donde  es una constante positiva; además, la ley de Newton establece que
es una constante positiva; además, la ley de Newton establece que 
a) Resuelva esta ecuación diferencial para determinar la velocidad en el tiempo  .
.
b) ¿Cuál es la velocidad límite?
c) Determine la distancia del objeto que cae, después de  segundos.
segundos.
51
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

Ecuaciones exactas.
1- Determine si cada ecuación diferencial es exacta:

2- Determine si la ecuación diferencial es exacta. Si es así, resuélvala:

52
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

3- Resuelva el problema con valor inicial:

4- Muestre que la ecuación dada no es exacta, pero que se convierte en exacta cuando se multiplica por el factor integrante especificado. Después, resuelva la ecuación.

5- Encuentre un factor integrante y después resuelva la ecuación:

53
SECCIÓN I: Ecuación Diferencial Ordinaria Lineal de Primer Orden

6- Pruebe que toda ecuación diferencial separable es exacta.
54

SECCIÓN II
Ecuación Diferencial Ordinaria Lineal
de Orden Superior
"Uno no puede discutir con un
teorema matemático"
Stephen Hawking
56
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
2. Ecuación Diferencial Ordinaria Lineal (EDO L) de Orden Superior.
Es aquélla que se puede escribir de la siguiente forma:

Salvo casos especiales, los métodos de resolución de ED de orden n > 1 son complicados y en muchos de ellos no es posible obtener una solución exacta, debiéndose emplear métodos numéricos para alcanzar soluciones aproximadas. En este libro sólo se tratarán las denominadas con coeficientes constantes.
Ecuación Diferencial Ordinaria Lineal de orden n con coeficientes constantes (EDO L cc).
Es aquélla que se puede escribir como:

En el caso particular que  , la ecuación anterior se
, la ecuación anterior se
57
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
denomina homogénea (EDO LH cc).
2.1. Teoremas sobre EDO L de orden n.
Teorema 1: Condición suficiente para la unicidad de la solución de una EDO L cc con valores iniciales.
H) Dado el sistema formado por una EDO L cc de orden n y n condiciones iniciales, donde  es continua en
es continua en  ,
,  .
.

T) Existe una única función  que satisface el sistema en
que satisface el sistema en  .
.
58
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Nota: Cuando un teorema de este texto carece del ícono  no será demostrado debido a que escapa a las posibilidades de este curso.
no será demostrado debido a que escapa a las posibilidades de este curso.
El teorema 1 (que en realidad es válido cuando  son funciones continuas en algún intervalo
son funciones continuas en algún intervalo  ) permite concluir que la solución general de
) permite concluir que la solución general de  será una ecuación que contiene n parámetros, los que luego se determinarán usando las n condiciones iniciales.
será una ecuación que contiene n parámetros, los que luego se determinarán usando las n condiciones iniciales.
Teorema 2: Principio de la superposición.

H)  es solución de:
es solución de:

 es solución de:
es solución de:

T)  es solución de:
es solución de:

59
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Teorema 3: Existencia de n funciones linealmente independientes que son solución de la EDO LH cc de orden n.
H) Dada:

T) Existen n funciones linealmente independientes que la solucionan.
Teorema 4: Combinación lineal de las soluciones de una EDO homogénea.

H)  e
e  soluciones de:
soluciones de:

 y
y  constantes cualesquiera;
constantes cualesquiera;  funciones continuas en algún intervalo
funciones continuas en algún intervalo  .
.
T)  también es solución de:
también es solución de:

60
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
2.2. EDO Lineal Homogénea con coeficientes constantes (EDO LH cc).
Combinando los teoremas anteriores es posible concluir que para encontrar la solución de una EDO LH de orden n es suficiente encontrar n funciones  linealmente independientes. La solución general será
linealmente independientes. La solución general será  constantes.
constantes.
Teorema 5: La ecuación característica.

H) T)  es solución de:
es solución de:

 es solución de la ecuación:
es solución de la ecuación:
La ecuación  se denomina ecuación característica, y a su primer miembro, polinomio característico.
se denomina ecuación característica, y a su primer miembro, polinomio característico.
61
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Dado que se trabajará sólo con  , será un polinomio de grado n, luego por el teorema fundamental del álgebra se sabe tiene n raíces; las que pueden ser reales o complejas, simples o múltiples. Se denominará
, será un polinomio de grado n, luego por el teorema fundamental del álgebra se sabe tiene n raíces; las que pueden ser reales o complejas, simples o múltiples. Se denominará  a dichas raíces.
a dichas raíces.
Si las n raíces son distintas se cuenta entonces con las n soluciones linealmente independientes necesarias para formar la solución general (notar que si  la única solución de
la única solución de  es
es  y
y  , luego
, luego  y
y  son linealmente independientes). De lo contrario, si alguna de las raíces tuvieran orden de multiplicidad mayor a 1, deberán encontrarse las funciones faltantes para completar las necesarias n.
son linealmente independientes). De lo contrario, si alguna de las raíces tuvieran orden de multiplicidad mayor a 1, deberán encontrarse las funciones faltantes para completar las necesarias n.
Además, para el caso que las raíces sean complejas, deberán realizarse algunas consideraciones para que las soluciones aportadas por este teorema conserven el tratamiento de la EDO en el campo de los reales. Se tratarán a continuación los cuatro tipos posibles de raíces del polinomio característico con coeficientes reales, explorando en primer lugar el caso particular de la de orden 2.
62
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Teorema 6: Solución general de la EDO LH de segundo orden con coeficientes reales constantes, según el tipo de raíces de su polinomio característico.

H)  ;
;  y
y  y
y  raíces de
raíces de 
T) a)  y
y  raíces reales distintas de
raíces reales distintas de
b) 
c)  raíces complejas conjugadas
raíces complejas conjugadas
 Ejemplos
Ejemplos
El teorema 6 puede generalizarse para una ecuación diferencial ordinaria lineal y homogénea de orden n con coeficientes constantes reales a través del teorema 7.
63
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Teorema 7: Solución general de la EDO LH cc reales constantes de orden n.
H) ;
; 
 polinomio
polinomio
característico de la EDO LH.
T) La solución general tendrá n sumandos que se determinarán con las siguientes reglas:
a) Por cada raíz real simple  de
de  la solución general tendrá un sumando:
la solución general tendrá un sumando:

b) Por cada par de raíces complejas simples  de
de  la solución general tendrá 2 sumandos:
la solución general tendrá 2 sumandos:

64
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
c) Por cada raíz real  de orden de multiplicidad k de
de orden de multiplicidad k de  la solución tendrá k sumandos de la forma:
la solución tendrá k sumandos de la forma:
d) Por cada par de raíces complejas múltiples de orden de multiplicidad k , la solución general tendrá 2k sumandos del tipo:
de orden de multiplicidad k , la solución general tendrá 2k sumandos del tipo:

 Ejemplos
Ejemplos
2.3. EDO de orden superior No Homogénea con coeficientes constantes (EDO L NH cc).
Recordar que no homogénea implica que f(x) no es la función nula. Se mostrará ahora que para determinar todas las
65
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
soluciones de una EDO Lineal no homogénea (ya sea con coeficientes constantes o variables), solamente se necesita hallar una solución de ella y la solución general de su homóloga homogénea.
Teorema 8: Solución general de EDO lineal no homogénea de orden n.

H)  y
y  funciones continuas en
funciones continuas en 
 e
e  son soluciones de
son soluciones de

 (1)
(1)
 es solución general de
es solución general de

 (2)
(2)
T)  es solución de:
es solución de:

Se usará el teorema anterior para el caso en que todas las 
66
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
son constantes, luego, será válido en el intervalo donde f(x) sea continua. Este teorema permite centrar la atención en la búsqueda de una solución propia  ; solución de
; solución de  ; dado que la solución de
; dado que la solución de  se determina fácilmente como se hizo en la subsección 2.2.
se determina fácilmente como se hizo en la subsección 2.2.
Notar que esta última solución aporta las n constantes necesarias para formar la solución general.
Existen dos métodos, cada uno con sus ventajas y desventajas. Para usar cualquiera de ellos la solución de la homogénea  juega un papel importante.
juega un papel importante.
1)Variación de los parámetros o de las constantes: tiene por ventaja su generalidad, es decir que se aplica a cualquier EDO L NH cc. Consiste en transformar la EDO en un sistema de n ecuaciones donde las n incógnitas son funciones. El obstáculo en su aplicación está asociado a cálculos tediosos.
2)Coeficientes a determinar: lleva corrientemente a cálculos
67
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
sencillos pero tiene por desventaja su particularidad, dado que sólo se aplica a algunas EDO, aquéllas en las que intervienen funciones f(x) cuyas derivadas tienen formas semejantes a f(x).
2.3.1. Variación de los parámetros
Se demostrará este método para una EDO de segundo orden, y luego se generalizará para una de orden n.
 Ejemplos
Ejemplos
68
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Teorema 9: Método de variación de los parámetros para 

H)  ;
;  soluciones Li de
soluciones Li de 
Existen dos funciones derivables  tales que solucionan:
tales que solucionan:

T)  es solución de:
es solución de:

Usando una demostración similar al caso particular de una EDO de orden 2 hecho anteriormente puede probarse el siguiente teorema.
69
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Teorema 10: Método de variación de los parámetros para una EDO L de orden n.
H)  soluciones Li de
soluciones Li de 
 n funciones derivables
n funciones derivables  tales que:
tales que:

T)  es solución de:
es solución de:
 , no siendo
, no siendo  la función nula.
la función nula.
Este teorema da las herramientas para resolver una EDO L NH
70
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
de orden cualquiera. Notar que  es un sistema lineal cuyas incógnitas son
es un sistema lineal cuyas incógnitas son  ;
;  . Los coeficientes del sistema lineal son las funciones que generan el espacio solución de la EDO homogénea asociada y las
. Los coeficientes del sistema lineal son las funciones que generan el espacio solución de la EDO homogénea asociada y las  primeras derivadas de cada una. El sistema
primeras derivadas de cada una. El sistema  puede ser escrito de la forma matricial como
puede ser escrito de la forma matricial como

Al determinante de la matriz M se lo denomina Wronskiano y puede mostrarse que es no nulo si y sólo si el conjunto formado por las n  son linealmente independientes (lo que en el teorema 10 está garantizado por hipótesis). Esto conlleva que el sistema
son linealmente independientes (lo que en el teorema 10 está garantizado por hipótesis). Esto conlleva que el sistema  sea compatible determinado y permite encontrar las n funciones
sea compatible determinado y permite encontrar las n funciones  . Integrándolas se obtienen las
. Integrándolas se obtienen las  buscadas.
buscadas.
71
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
 Ejemplos
Ejemplos
Luego de los ejemplos anteriores puede notarse que este método es eficaz, dado que, siempre que se conozcan las soluciones de la ecuación característica, es posible resolver la EDO L NH, cualquiera sea la f(x). Sin embargo, aún en casos sencillos, necesita de numerosos cálculos, muchas veces engorrosos. Sin embargo son algoritmizables, por lo que los SAC lo utilizan.
Por fortuna, para las f(x) más frecuentes en problemas de física e ingeniería, es posible utilizar un método más eficiente ya que logra resolver las EDO con menos cálculos, denominado coeficientes indeterminados, el que se desarrollará en el apartado 2.3.2.
2.3.2. Coeficientes a determinar (o coeficientes indeterminados).
Como se expresó anteriormente, este método es una regla particular para resolver la ecuación:
72
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior

Se podrá usar sólo si  tiene la forma:
tiene la forma:  , siendo
, siendo  y
y  ; polinomios de grado
; polinomios de grado  y
y  respectivamente y
respectivamente y  y
y  constantes.
constantes.
Notar que  puede tener distintas formas de acuerdo a los diferentes parámetros, muchas de ellas presentes frecuentemente en ecuaciones que modelan problemas reales de economía, ingeniería o biología. Por ejemplo:
puede tener distintas formas de acuerdo a los diferentes parámetros, muchas de ellas presentes frecuentemente en ecuaciones que modelan problemas reales de economía, ingeniería o biología. Por ejemplo:  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Se aplica para dichas funciones porque ellas tienen derivadas que conservan sus características al derivar, esto es, una combinación lineal de sus derivadas tendrá la misma forma. Este método consiste en plantear una solución que se “sospecha” factible. Se ilustrará el método con algunos ejemplos sobre cómo elegir dicha función, para luego formalizar la elección.
73
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
 Ejemplos
Ejemplos
El éxito del método ''coeficientes a determinar'' para encontrar la solución propia de una EDO L N H cc depende de la correcta elección de la solución propuesta. Para una buena elección, plantear una forma análoga a f (x) y compararla con la solución característica. Si alguno o todos los t érminos están contenidos en ella, se la debe multiplicar por x
( ¡y repetir el procedimiento! )
 Ejemplo
Ejemplo
Formalización de las reglas para proponer la solución propia de la ecuación (1):
74
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior

I) Si  polinomios de grado n.
polinomios de grado n.
II) Si 

Siendo  y
y  polinomios de grado
polinomios de grado  y
y  respectivamente;
respectivamente;  y
y  polinomios de grado
polinomios de grado  .
.
III) Si luego de aplicar las dos reglas anteriores algún sumando de  está contenido en la solución complementaria multiplique la
está contenido en la solución complementaria multiplique la  anterior por el factor
anterior por el factor  , donde
, donde  es el menor entero positivo tal que ningún término
es el menor entero positivo tal que ningún término pertenece a
pertenece a  .
.
 Ejemplos
Ejemplos
75
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
Ejercitación propuesta.
1- Resuelva las siguientes ecuaciones diferenciales:

2- Resuelva el problema con valor inicial:

76
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior

3- Resuelva, si fuese posible, cada problema con valor en la frontera:

4- a) Demuestre que el problema con valor en la frontera  , tiene sólo la solución trivial
, tiene sólo la solución trivial  , para los casos
, para los casos  y
y  .
.
b) Para el caso  , determine los valores de
, determine los valores de  para los que este problema tiene una solución distinta de la trivial, y proporcione la solución correspondiente.
para los que este problema tiene una solución distinta de la trivial, y proporcione la solución correspondiente.

77
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
5- Resuelva la ecuación diferencial o el problema con valor inicial, utilizando el método de los coeficientes indeterminados.

78
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior
6- Escriba una solución propuesta para el método de los coeficientes indeterminados. No determine los coeficientes:

7- Resuelva la ecuación diferencial utilizando: (a) coeficientes indeterminados, y (b) variación de parámetros:

8- Resuelva la ecuación diferencial empleando el método de la variación de parámetros:

79
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior

9- Optativo: Mostrar, utilizando al menos dos métodos, que  es una solución propia de
es una solución propia de  . Ayuda: Resolver verificando y usando variación de los parámetros.
. Ayuda: Resolver verificando y usando variación de los parámetros.
10- Seguramente el lector notó que al determinar las  en el método de variación de los parámetros usando
en el método de variación de los parámetros usando  se omitió en la resolución de las integrales la constante de integración. Dar razones para dicha omisión.
se omitió en la resolución de las integrales la constante de integración. Dar razones para dicha omisión.
11- Resolver usando coeficientes indeterminados y variación de los parámetros las EDO:

80
SECCIÓN II: Ecuación Diferencial Ordinaria Lineal de Orden Superior

12- Movimiento del proyectil en un medio viscoso: Encontrar la posición  del proyectil de masa
del proyectil de masa  disparado desde
disparado desde  con rapidez
con rapidez  y ángulo sobre la horizontal
y ángulo sobre la horizontal  , suponiendo que después de disparado, además de la fuerza gravitacional existe una de rozamiento que es proporcional y opuesta a la velocidad
, suponiendo que después de disparado, además de la fuerza gravitacional existe una de rozamiento que es proporcional y opuesta a la velocidad  . Utilizar un SAC para comparar las trayectorias iguales a
. Utilizar un SAC para comparar las trayectorias iguales a  y
y  con y sin rozamiento.
con y sin rozamiento.


81

SECCIÓN III
Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
"Si la gente no piensa que
las matemáticas son simples,
es sólo porque no se da cuenta
de lo complicada que es la vida"
John Von Neumann
84
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
3. Sistema lineal de EDO con coeficientes constantes.
Hasta el momento, se ha estudiado la solución de una EDO L (con o sin los datos de valores iniciales, dando por resultado una familia solución o una única solución, dependiendo del caso). Ahora se tratará el problema referido a la resolución de sistemas EDO lineales, esto es, encontrar las funciones que solucionan simultáneamente un conjunto de ED.
Normalmente esos sistemas aparecen en modelos que involucran determinar más de una función de la misma variable independiente, la que normalmente suele ser el tiempo. Por ejemplo, determinar la posición de un móvil sujeto a un campo de velocidad conocido, o determinar la concentración de un químico en distintos tanques comunicados entre sí. En esta sección se asumirá como variable independiente a  y como funciones incógnita a
y como funciones incógnita a  ;
;  (en general,
(en general,  ); aunque, para facilitar la notación, se omitirá indicar la dependencia de
); aunque, para facilitar la notación, se omitirá indicar la dependencia de  , nombrando las funciones incógnita como
, nombrando las funciones incógnita como  y
y  . Hay métodos muy sencillos que permiten transformar
. Hay métodos muy sencillos que permiten transformar
85
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
un sistema lineal de cualquier orden en uno de primer orden; por ello, se tratarán sólo éstos.
En esta sección se resolverán sistemas lineales de ecuaciones diferenciales (SL EDO) por de dos métodos, uno denominado método de eliminación y el otro, matricial.
3.1. Resolución de SL EDO por método de eliminación.
El nombre de este método elemental proviene del hecho que transforma el SL EDO en otro, pero que posee una incógnita de orden superior de una única función incógnita. Esto se puede resolver usando los procedimientos de la sección II. Consiste en despejar de una de la ecuaciones una de las funciones y reemplazarla en las otras, obteniendo así un nuevo sistema con una ecuación menos. Se repite la operación hasta lograr una única ecuación lineal.
 Ejemplos
Ejemplos
Habrá notado el lector, a partir de los ejemplos, que este
86
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
procedimiento resulta muy laborioso, lo que justifica indagar en un método más eficiente y sistemático para resolver sistemas similares a éste. Se tratará el mismo problema en la subsección 3.2. con el uso del álgebra lineal.
3.2. Resolución de SL EDO usando matriz exponencial: uso del Álgebra Lineal
3.2.1. Sistemas Homogéneos.
Suponer el sistema:

donde  (aunque podrían ser funciones continuas, sólo se trabajará con constantes reales). El mismo se puede escribir de la forma matricial:
(aunque podrían ser funciones continuas, sólo se trabajará con constantes reales). El mismo se puede escribir de la forma matricial:
87
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes

o en su forma vectorial:

Si  son soluciones del sistema
son soluciones del sistema  y, además, el conjunto es linealmente independiente, se lo denomina conjunto fundamental de soluciones.
y, además, el conjunto es linealmente independiente, se lo denomina conjunto fundamental de soluciones.
Observar la similitud de  con la ecuación de Abel
con la ecuación de Abel  , la que tiene por solución desarrollando en serie:
, la que tiene por solución desarrollando en serie:

El segundo teorema de esta sección mostrará que una expresión similar es la solución del sistema de EDO.
88
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Matriz exponencial
Se comenzará por la definir conceptos necesarios del álgebra lineal. Sea la matriz cuadrada  , se denomina matriz exponencial a la matriz:
, se denomina matriz exponencial a la matriz:

Luego:
 Ejemplos
Ejemplos
Teorema 1: Convergencia de la matriz exponencial  .
.
H)
T)  es convergente para todo
es convergente para todo  .
.
89
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Teorema 2: Solución general de un sistema lineal de ecuaciones diferenciales (forma matricial).
H) , con coeficientes reales
, con coeficientes reales
 función vectorial derivable sobre
función vectorial derivable sobre 
 cuyas componentes son constantes cualesquiera.
cuyas componentes son constantes cualesquiera.
T)  es solución de
es solución de 
Observaciones:
Si se conoce la condición inicial  se puede determinar fácilmente el valor de
se puede determinar fácilmente el valor de  pues
pues  . De forma similar, mostrar la segunda afirmación del teorema 3.
. De forma similar, mostrar la segunda afirmación del teorema 3.
90
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Teorema 3: Solución particular de un sistema lineal de ecuaciones diferenciales (forma matricial).
La solución particular de  es
es  y la de
y la de  es
es 
Este teorema da el procedimiento para encontrar la solución particular del sistema  si se conoce la condición inicial
si se conoce la condición inicial  .
.
El método se reduce a calcular la matriz  , denominada matriz fundamental del sistema o solución matricial fundamental. La complejidad de la determinación
, denominada matriz fundamental del sistema o solución matricial fundamental. La complejidad de la determinación  depende de
depende de  .
.
Por orden de complejidad, se tratarán los tres casos posibles:
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
3.2.1.1.  es diagonal.
es diagonal.
La solución es  .
.
 Ejemplo
Ejemplo
3.2.1.2.  no es diagonal, pero es diagonalizable.
no es diagonal, pero es diagonalizable.
Tampoco es difícil utilizar el teorema 3 si la matriz  es diagonalizable, esto es, existe la matriz invertible
es diagonalizable, esto es, existe la matriz invertible  tal que
tal que  .
.
Bajo estas condiciones  y
y  .
.

92
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Reescribiendo:

Notando que cada sumando de la serie tiene como primera matriz del producto a  y última a
y última a  , se extraen ellas como factores comunes:
, se extraen ellas como factores comunes:


Luego,

 Ejemplos
Ejemplos
93
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
3.2.1.3. La matriz  no es diagonalizable.
no es diagonalizable.
Aquí es necesario recurrir a la forma canónica de Jordan de la matriz  . Así, puede mostrarse que existe la matriz
. Así, puede mostrarse que existe la matriz  tal que
tal que  .
.
Se tratará sólo el caso  , no diagonalizable. El polinomio característico tiene dos raíces iguales
, no diagonalizable. El polinomio característico tiene dos raíces iguales  y
y  tiene un único autovector
tiene un único autovector  . Se demuestra en cursos avanzados de Álgebra Lineal que el segundo vector columna de
. Se demuestra en cursos avanzados de Álgebra Lineal que el segundo vector columna de  se obtiene de la ecuación
se obtiene de la ecuación  . Este sistema tiene infinitas soluciones; se debe adoptar una no nula. Además,
. Este sistema tiene infinitas soluciones; se debe adoptar una no nula. Además,  , y
, y  .
.
Finalmente,  .
.
Luego,  .
.
 Ejemplo
Ejemplo
94
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
3.2.2. Sistemas No Homogéneos.
Se verá un método para resolver los SL EDO que respondan a la forma  .
.
Teorema 4:
H)  y
y  son soluciones del sistema no homogéneo
son soluciones del sistema no homogéneo  (1)
(1)
T)  es solución del sistema homogéneo
es solución del sistema homogéneo  (2)
(2)
Esto significa que  . Advierta la similitud del teorema 4 con el
. Advierta la similitud del teorema 4 con el  , denominando
, denominando  a la solución general del sistema homogéneo.
a la solución general del sistema homogéneo.
95
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Luego:

Esto significa que cualquier solución del sistema no homogéneo puede expresarse como la suma de la solución del sistema homogéneo más una propia. Así, la solución general del sistema no homogéneo  será
será  , siendo
, siendo  y
y  una solución propia.
una solución propia.
La solución general de  es:
es:  .
.
Para la determinación de la solución propia  de un SL EDO de primer orden se demostrará el siguiente teorema:
de un SL EDO de primer orden se demostrará el siguiente teorema:
96
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Teorema 5:Método de variación de las constantes para determinar la solución propia.

H) Dada  ;
;  matriz cuadrada de tamaño n ;
matriz cuadrada de tamaño n ;  con funciones componentes continuas.
con funciones componentes continuas.
T) 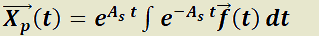 es solución propia del sistema no homogéneo.
es solución propia del sistema no homogéneo.
 es solución
es solución
general de  .
.
 Ejemplos
Ejemplos
97
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Si se quiere resolver el sistema no homogéneo con valor inicial
con valor inicial  , no es difícil comprobar que la solución será:
, no es difícil comprobar que la solución será:
 (*)
(*)
Notar que .
.
Entonces:

ya que  es una constante para la integral.
es una constante para la integral.
Así:

Si se deriva m.a m. se tiene, usando las reglas de derivación de la exponencial y la derivada de un producto:
98
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes

Por el teorema fundamental de las integrales definidas, . Luego:
. Luego:

Sacando factor común la matriz  entre los dos primeros sumandos y considerando que la inversa de
entre los dos primeros sumandos y considerando que la inversa de  es
es  :
:


Luego, verifica la ecuación  .
.
99
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Si se evalúa en
en :
:

 , que verifica la ecuación (*).
, que verifica la ecuación (*).
La solución de la ecuación con valor inicial
 es:
es:
 .
.
 Ejemplos
Ejemplos
100
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Los ejemplos desarrollados en esta sección usando el álgebra lineal seguramente plantean interrogantes al lector. Uno de ellos es que las fórmulas demostradas requieren tediosos cálculos entre matrices, especialmente si éstas son de orden mayor que dos. Sin embargo ésta es muy útil ya que los cálculos pueden eludirse al traducirlos en un algoritmo sencillo de programar en un sistema algebraico de cómputos.
Otro interrogante es que dicha fórmula sólo permite resolver el problema si las condiciones iniciales con las que se cuenta valorizan todas las incógnitas (componentes de  ) en el mismo valor de
) en el mismo valor de  . Si se conocen los valores iniciales de las componentes (o incluso de una derivada) en distintos valores de la variable, el problema se resuelve determinando primero la solución general, para luego encontrar las constantes.
. Si se conocen los valores iniciales de las componentes (o incluso de una derivada) en distintos valores de la variable, el problema se resuelve determinando primero la solución general, para luego encontrar las constantes.
 Ejemplo
Ejemplo
101
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
Ejercitación propuesta.
Utilizando los métodos de eliminación y matricial resolver los sistemas planteados.
1- Dado  ; siendo
; siendo  ;
;  .
.
a) Dar la matriz fundamental.
b) Resolver el sistema.

2. Dado  ; siendo
; siendo  y
y  constantes distintas.
constantes distintas.
a) Dar la solución matricial fundamental.
102
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
b) Resolver el sistema

3- Dado  ; siendo
; siendo  ;
; .
.
a) Dar la matriz fundamental.
b) Resolver S.

4. Dado el sistema  (necesita usar forma de Jordan)
(necesita usar forma de Jordan)
103
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes
a) Calcular la solución general.
b) Mostrar que  es solución.
es solución.

5- Encontrar la solución general de:  (autovalores imaginarios).
(autovalores imaginarios).

6. Dado  (autovalores complejos). Calcular:
(autovalores complejos). Calcular:
a) La solución general.
b) La solución particular que verifica  y
y  .
.
104
SECCIÓN III: Sistema Lineal de Ecuaciones Diferenciales Ordinarias con coeficientes constantes

7. Dado  ; calcular:
; calcular:
a) La solución general.
b) La solución particular, siendo 
 .
.


105

SECCIÓN IV
Teoría Cualitativa
"Parece que uno de los rasgos fundamentales de la naturaleza
es que las leyes físicas fundamentales
se describen en términos de
una teoría matemática de gran belleza y poder,
para comprender la cual se necesita
una norma muy elevada de matemáticas...
Uno quizás puediera decribir la situación diciendo que
Dios es un matemático de orden muy elevado,
y que Él usó matemática muy adelantada
para construir el universo"
Paul Dirac
108
SECCIÓN IV: Teoría Cualitativa
4. Teoría Cualitativa.
En matemática es importante estudiar la estabilidad de las soluciones de ED, es decir, cómo difieren las soluciones bajo pequeñas modificaciones de las condiciones iniciales. Dicha estabilidad es muy importante en la ciencia que utilice la ED (por ejemplo, en la Física), ya que, en la realidad, las condiciones iniciales normalmente no se conocen con certeza (datos obtenidos con aparatos de poca precisión), y es importante que pequeños cambios de las mismas no generen comportamientos cualitativos diferentes en la solución encontrada.
Cuando la diferencia entre dos soluciones con valores iniciales cercanos es cualitativamente grande se dice que el sistema no presenta estabilidad, y, por supuesto, en ingeniería no se valora positivamente esta situación.
Debido a que toda ED de orden superior puede reducirse a un sistema de ecuaciones diferenciales (SED) de primer orden equivalente, el estudio de la estabilidad de las soluciones de ED puede reducirse al estudio de la estabilidad de los SED.
109
SECCIÓN IV: Teoría Cualitativa
Si bien el análisis se puede hacer para un sistema de n ecuaciones, dado que interesa utilizar características gráficas de la solución, el tratamiento se hará para sistemas con dos incógnitas.
4.1. Estabilidad de los sistemas lineales.
Hasta ahora, el estudio de las ED y SED se ha centrado en el problema de obtener analíticamente las soluciones exponiendo algunos métodos de resolución de ciertos tipos de ecuaciones y sistemas.
Interesa ahora dar otro enfoque, esto es obtener información “cualitativa” sobre el comportamiento de las soluciones. Se usarán ejemplos para caracterizarlo. La solución buscada será interpretada como líneas de flujo de campos de velocidad. Los ejemplos, aún teniendo enunciados similares, arrojarán soluciones muy distintas entre sí. Luego, los resultados obtenidos serán motivo de análisis en la subsección 4.2.
 Ejemplos
Ejemplos
110
SECCIÓN IV: Teoría Cualitativa
4.2. Punto de equilibrio de un sistema lineal. Estabilidad.
Sistemas autónomos y no autónomos.
Dado el sistema bidimensional , se dice que es autónomo si
, se dice que es autónomo si  e
e  no dependen explícitamente de
no dependen explícitamente de  (tiempo). Por ejemplo,
(tiempo). Por ejemplo,  es autónomo mientras que
es autónomo mientras que  no lo es. Note que los sistemas lineales homogéneos son autónomos, mientras que los no homogéneos no, excepto que
no lo es. Note que los sistemas lineales homogéneos son autónomos, mientras que los no homogéneos no, excepto que  .
.
Plano de Fase y Órbita.
La solución de un SED de dos ecuaciones con dos funciones incógnita con condiciones iniciales dadas es una pareja de funciones  . Para representar gráficamente la solución del sistema frecuentemente se utiliza la curva
. Para representar gráficamente la solución del sistema frecuentemente se utiliza la curva
111
SECCIÓN IV: Teoría Cualitativa
paramétrica. A la curva se la denomina órbita o trayectoria, mientras que al plano  , plano de fase.
, plano de fase.
Las órbitas suelen brindar, codificada, mucha información del sistema. El estudiante puede apreciar que en los ejemplos de la subsección 4.1. se graficaron órbitas de sistemas lineales bajo la interpretación de líneas de flujo.
Puede observarse que es una característica de los sitemas autónomos que la órbita no depende del valor inicial  , pero sí del valor
, pero sí del valor  . A modo de ejemplo, en la simulación siguiente se representan las órbitas del sistema
. A modo de ejemplo, en la simulación siguiente se representan las órbitas del sistema  con condiciones iniciales
con condiciones iniciales  ; particularizando con
; particularizando con  ,
,  y
y  .
.

112
SECCIÓN IV: Teoría Cualitativa
Note que en todos los casos la representación gráfica de la órbita es la misma, sea ésta  o
o  . Si se consideraran trayectorias de tres móviles, éstos recorrerían el mismo camino, pero encontrándose cada uno en distintos puntos del plano en un instante dado.
. Si se consideraran trayectorias de tres móviles, éstos recorrerían el mismo camino, pero encontrándose cada uno en distintos puntos del plano en un instante dado.
Por el contrario, la siguiente simulación muestra las órbitas del sistema no autónomo  con las condiciones iniciales
con las condiciones iniciales  ; particularizando con
; particularizando con  ,
,  y
y  .
.

Note que las órbitas son distintas (más allá que conserven alguna regularidad en su forma).
113
SECCIÓN IV: Teoría Cualitativa
Dado el sistema autónomo  , problema con valor inicial
, problema con valor inicial  , si
, si  y
y  son continuas y con derivadas parciales continuas entonces la existencia y unicidad de la solución está garantizada.
son continuas y con derivadas parciales continuas entonces la existencia y unicidad de la solución está garantizada.
Dado que las órbitas de cualquier sistema general autónomo son independientes de  supondremos por simplicidad
supondremos por simplicidad  .
.
Punto crítico.
Se denomina punto crítico  del sistema autónomo de primer orden
del sistema autónomo de primer orden  , si
, si  .
.
Note que  es una solución, estable o de equilibrio, del problema con valor inicial ya que la verifica:
es una solución, estable o de equilibrio, del problema con valor inicial ya que la verifica:  . Esto significa que si se suelta una partícula
. Esto significa que si se suelta una partícula
114
SECCIÓN IV: Teoría Cualitativa
en  en un campo de velocidades
en un campo de velocidades  , ésta permanecerá en reposo ya que la velocidad
, ésta permanecerá en reposo ya que la velocidad  . Pero interesan las demás soluciones de
. Pero interesan las demás soluciones de  (cuando las condiciones iniciales no son
(cuando las condiciones iniciales no son  ).
).
Es por ello que a un punto crítico se lo denomina punto de equilibrio del sistema.
 Ejemplos
Ejemplos
Estabilidad del punto crítico.
Se dará una definición no formal, pero intuitiva, de estabilidad del punto crítico en la que se hará referencia a “cercanía” entendiendo como tal "dentro de un círculo de radio finito".
115
SECCIÓN IV: Teoría Cualitativa
Se dice que el punto crítico  del sistema es estable si una trayectoria que está “cerca” del mismo en el instante
del sistema es estable si una trayectoria que está “cerca” del mismo en el instante  permanecerá “cerca” de él para todo
permanecerá “cerca” de él para todo  .
.
Se dice que el punto crítico  del sistema es asintóticamente estable, cuando es estable y las trayectorias se aproximan al punto conforme aumenta
del sistema es asintóticamente estable, cuando es estable y las trayectorias se aproximan al punto conforme aumenta  . Esto es, si
. Esto es, si  , entonces
, entonces  e
e  . Éste es un caso particular de estabilidad.
. Éste es un caso particular de estabilidad.
Se dice que el punto crítico  del sistema es inestable cuando no es estable. Esto significa que las trayectorias que empiezan cerca del punto de equilibrio se alejan de él a medida que transcurre el tiempo, es decir, cuando la variable independiente
del sistema es inestable cuando no es estable. Esto significa que las trayectorias que empiezan cerca del punto de equilibrio se alejan de él a medida que transcurre el tiempo, es decir, cuando la variable independiente  .
.
Retomando los ejemplos de la  del ejemplo N° 8 es estable, mientras que el punto crítico
del ejemplo N° 8 es estable, mientras que el punto crítico  es inestable. Use Da Vinci y advierta que si la
es inestable. Use Da Vinci y advierta que si la
116
SECCIÓN IV: Teoría Cualitativa
partícula se deposita en  (use condiciones iniciales
(use condiciones iniciales  ;
;  ), la misma permanecerá en reposo dado que este punto es un punto de equilibrio. Sin embargo, si se realiza un pequeño cambio en las condiciones iniciales, la misma seguirá una trayectoria cerrada, que estará dentro de un circunferencia de radio finito. Ello se debe a que este punto es de equilibrio estable. Si en el mismo campo se deposita la partícula en el otro punto crítico
), la misma permanecerá en reposo dado que este punto es un punto de equilibrio. Sin embargo, si se realiza un pequeño cambio en las condiciones iniciales, la misma seguirá una trayectoria cerrada, que estará dentro de un circunferencia de radio finito. Ello se debe a que este punto es de equilibrio estable. Si en el mismo campo se deposita la partícula en el otro punto crítico  no se moverá, pero si se la desplaza (muy poquito), la misma seguirá una trayectoria que se alejará indefinidamente del punto. Note que las gráficas de series de tiempo muestran que tanto
no se moverá, pero si se la desplaza (muy poquito), la misma seguirá una trayectoria que se alejará indefinidamente del punto. Note que las gráficas de series de tiempo muestran que tanto  como
como  son funciones acotadas en el primer caso, mientras que al menos una de ellas no lo es en el segundo caso. En el ejemplo N° 9 el único punto crítico es inestable, mientras que en el ejemplo N° 10 los infinitos puntos críticos son asintóticamente estables.
son funciones acotadas en el primer caso, mientras que al menos una de ellas no lo es en el segundo caso. En el ejemplo N° 9 el único punto crítico es inestable, mientras que en el ejemplo N° 10 los infinitos puntos críticos son asintóticamente estables.
En lo que sigue, el estudio se centrará en dos cuestiones que constituyen una parte esencial del plano de fase de los sistemas lineales autónomos:
— La disposición de las trayectorias cerca del punto crítico  .
.
117
SECCIÓN IV: Teoría Cualitativa
— La estabilidad o inestabilidad del punto crítico  .
.
Clasificación de los puntos de equilibrio en sistemas lineales homogéneos.
Se verá que la naturaleza y estabilidad del punto crítico queda caracterizada por los autovalores de la matriz  del sistema. Si
del sistema. Si  es su único punto crítico, equivale a decir que
es su único punto crítico, equivale a decir que  y por ello que los autovalores
y por ello que los autovalores  y
y  son no nulos simultáneamente. En función del comportamiento de las trayectorias en relación con el punto crítico aislado
son no nulos simultáneamente. En función del comportamiento de las trayectorias en relación con el punto crítico aislado  , éste se denominará:
, éste se denominará:
Nodo
El punto crítico es un nodo si los autovalores  y
y  son reales y del mismo signo. Las órbitas son similares a semirrectas o
son reales y del mismo signo. Las órbitas son similares a semirrectas o
118
SECCIÓN IV: Teoría Cualitativa
parábolas.
 Simulador DaVinci—
Simulador DaVinci—  negativos: “el móvil” se acerca al origen. El equilibrio es asintóticamente estable. Se puede apreciar este hecho ejecutando el ejemplo Nº 4 de la galería de "Sistemas Autónomos" del simulador DaVinci.
negativos: “el móvil” se acerca al origen. El equilibrio es asintóticamente estable. Se puede apreciar este hecho ejecutando el ejemplo Nº 4 de la galería de "Sistemas Autónomos" del simulador DaVinci.
 Simulador DaVinci—
Simulador DaVinci—  positivos: “el móvil” se aleja del origen, el equilibrio es inestable. Se puede apreciar este hecho ejecutando el ejemplo N° 5 de la galería de "Sistemas Autónomos" del simulador DaVinci.
positivos: “el móvil” se aleja del origen, el equilibrio es inestable. Se puede apreciar este hecho ejecutando el ejemplo N° 5 de la galería de "Sistemas Autónomos" del simulador DaVinci.
 Simulador DaVinci—
Simulador DaVinci—  : el punto crítico suele recibir el nombre de nodo impropio. El ejemplo N° 10 de la galería de "Sistemas Autónomos" del simulador DaVinci muestra el caso de autovalores iguales negativos; en tanto que el ejemplo N° 11, autovalores iguales positivos.
: el punto crítico suele recibir el nombre de nodo impropio. El ejemplo N° 10 de la galería de "Sistemas Autónomos" del simulador DaVinci muestra el caso de autovalores iguales negativos; en tanto que el ejemplo N° 11, autovalores iguales positivos.
119
SECCIÓN IV: Teoría Cualitativa
Note que para los dos primeros casos  (en forma similar
(en forma similar  ), mientras que para el tercero
), mientras que para el tercero  (en forma similar
(en forma similar  ).
).
Punto de silla
 Simulador DaVinciEl punto crítico es un punto de silla si los autovalores
Simulador DaVinciEl punto crítico es un punto de silla si los autovalores  y
y  son reales y de distinto signo. Las órbitas, cuando
son reales y de distinto signo. Las órbitas, cuando  , se presentan como trayectorias que se acercan al origen al principio y luego se separan de él.
, se presentan como trayectorias que se acercan al origen al principio y luego se separan de él.
Esto permite concluir que todo punto de silla es inestable. Las trayectorias se asemejan a hipérbolas o semirrectas, como lo muestra el ejemplo N° 6 de la galería de "Sistemas Autónomos" del simulador DaVinci. Note que  (o
(o  ) responde también a la expresión
) responde también a la expresión  pero a diferencia del caso anterior los dos sumandos de
pero a diferencia del caso anterior los dos sumandos de  tienen comportamientos distintos para
tienen comportamientos distintos para  . Sin embargo, cuando el punto crítico es un punto de silla siempre
. Sin embargo, cuando el punto crítico es un punto de silla siempre  e
e  .
.
120
SECCIÓN IV: Teoría Cualitativa
Centro
 Simulador DaVinci El punto crítico es un centro cuando los autovalores son imaginarios puros. Las trayectorias son curvas cerradas que rodean al origen, que en general tienen forma de elipses, de modo que ninguna trayectoria tiende a él cuando
Simulador DaVinci El punto crítico es un centro cuando los autovalores son imaginarios puros. Las trayectorias son curvas cerradas que rodean al origen, que en general tienen forma de elipses, de modo que ninguna trayectoria tiende a él cuando  ó
ó  Por ello, el punto
crítico es estable, pero no asintóticamente estable. Ejecutar el ejemplo N° 3
de la galería de "Sistemas Autónomos".
Por ello, el punto
crítico es estable, pero no asintóticamente estable. Ejecutar el ejemplo N° 3
de la galería de "Sistemas Autónomos".
Foco
El punto crítico es un foco cuando los autovalores son complejos conjugados y tienen parte real no nula. Las órbitas son curvas en forma de espiral que, conforme  , pueden presentar dos situaciones:
, pueden presentar dos situaciones:  Simulador DaVinci
Simulador DaVinci
—  : las órbitas se acercan al origen; luego, el equilibrio es asintóticamente estable. Ejecutar el ejemplo N° 1 de la galería de
: las órbitas se acercan al origen; luego, el equilibrio es asintóticamente estable. Ejecutar el ejemplo N° 1 de la galería de
121
SECCIÓN IV: Teoría Cualitativa
"Sistemas Autónomos" del simulador DaVinci para apreciar este hecho.
—  Simulador DaVinci
Simulador DaVinci  : lás órbitas se separan del origen; luego, el equilibrio es inestable. Ejecutar el ejemplo N° 2 de la galería de "Sistemas Autónomos" del simulador DaVinci para apreciar este hecho.
: lás órbitas se separan del origen; luego, el equilibrio es inestable. Ejecutar el ejemplo N° 2 de la galería de "Sistemas Autónomos" del simulador DaVinci para apreciar este hecho.
A modo de síntesis, se propone completar la siguiente tabla:
Tabla Resumen para punto crítico aislado del sistema 

 Ejemplos
Ejemplos

122
SECCIÓN IV: Teoría Cualitativa
El punto crítico aislado del sistema lineal autónomo
es estable si y sólo si todos los autovalores tienen parte real no positiva ;
es asintóticamente estable si y sólo si todos los autovalores tienen parte real negativa ;
es inestable si existe al menos un autovalor con parte real positiva.
Importante :
la estabilidad de la solución de una ecuación diferencial ordinaria homogénea de orden n puede ser caracterizada por las n raíces de su
ecuación característica.
123
SECCIÓN IV: Teoría Cualitativa
Ejercitación propuesta
 Simulador DaVinci1- Sea el campo de velocidades
Simulador DaVinci1- Sea el campo de velocidades  .
.
a) Plantear el sistema de ecuaciones diferenciales que permiten determinar las trayectorias de flujo  .
.
b) Probar que dicho sistema puede reducirse a  ;
;  .
.
c) Resolver la primera ecuación del inciso anterior.
d) Encontrar la trayectoria de una partícula que parte del punto  .
.
e) En el gráfico se muestran tres trayectorias de flujo, una de ella es la buscada. Determinar la misma, justificando la respuesta.

125
SECCIÓN IV: Teoría Cualitativa

 Simulador DaVinci2- Un móvil se mueve siguiendo una trayectoria
Simulador DaVinci2- Un móvil se mueve siguiendo una trayectoria  , de tal manera que en todo
, de tal manera que en todo  su velocidad está dada por
su velocidad está dada por  . Si el móvil parte del punto
. Si el móvil parte del punto  :
:
a) Plantear el sistema de ecuaciones diferenciales que permiten determinar la trayectoria.
b) Probar que dicho sistema puede reducirse a las ecuaciones  ;
;  ;
;  .
.
c) Encontrar la trayectoria.
d) En el gráfico de la página 125 se muestran distintas trayectorias, una de ellas es la buscada. Determinar la misma, justificando la respuesta.
126
SECCIÓN IV: Teoría Cualitativa


 Simulador DaVinci3- Si los autovalores de la matriz del sistema lineal de ecuaciones diferenciales son todos positivos, ¿es estable el punto crítico del sistema y la órbita una espiral? Justificar.
Simulador DaVinci3- Si los autovalores de la matriz del sistema lineal de ecuaciones diferenciales son todos positivos, ¿es estable el punto crítico del sistema y la órbita una espiral? Justificar.

127
SECCIÓN IV: Teoría Cualitativa
 Simulador DaVinci4- Resolver el sistema
Simulador DaVinci4- Resolver el sistema  . Caracterizar el equilibrio de su punto crítico.
. Caracterizar el equilibrio de su punto crítico.

 Simulador DaVinci5- Una partícula se mueve en el plano
Simulador DaVinci5- Una partícula se mueve en el plano  con velocidad
con velocidad  . ¿Cuáles serán los valores de
. ¿Cuáles serán los valores de  para que la trayectoria de la partícula sea elíptica?
para que la trayectoria de la partícula sea elíptica?

 Simulador DaVinci6- Dado el sistema
Simulador DaVinci6- Dado el sistema  ; ¿existen valores de
; ¿existen valores de  para los cuales
para los cuales  ? Justificar.
? Justificar.

128
SECCIÓN IV: Teoría Cualitativa
 Simulador DaVinci7- Caracterizar el equilibrio del punto crítico y la órbita del sistema:
Simulador DaVinci7- Caracterizar el equilibrio del punto crítico y la órbita del sistema: 
 Simulador DaVinci8- Caracterizar el equilibrio del punto crítico y la órbita del sistema S:
Simulador DaVinci8- Caracterizar el equilibrio del punto crítico y la órbita del sistema S:

 Simulador DaVinci9- Hallar la solución general de los siguientes sistemas homogéneos, caracterizar el equilibrio del/los punto/s crítico/s e indicar la forma de la trayectoria solución (órbita):
Simulador DaVinci9- Hallar la solución general de los siguientes sistemas homogéneos, caracterizar el equilibrio del/los punto/s crítico/s e indicar la forma de la trayectoria solución (órbita):
a) 
b) 
129
SECCIÓN IV: Teoría Cualitativa
c) 
d) 
e) 

f)
130
SECCIÓN IV: Teoría Cualitativa
g) 
 Simulador DaVinci10- Escribir la forma general de
Simulador DaVinci10- Escribir la forma general de  y caracterizar el equilibrio del punto crítico de:
y caracterizar el equilibrio del punto crítico de:
a)
b)
 Simulador DaVinci11- Una partícula se soltará en el punto
Simulador DaVinci11- Una partícula se soltará en el punto  en un campo estable de velocidad
en un campo estable de velocidad  . ¿Existe/n valor/es de
. ¿Existe/n valor/es de  para el/los cual/es la trayectoria de la solución es una elipse? Justificar.
para el/los cual/es la trayectoria de la solución es una elipse? Justificar.
131
SECCIÓN IV: Teoría Cualitativa

 Simulador DaVinci12- Sea el campo de velocidades
Simulador DaVinci12- Sea el campo de velocidades  . Si una partícula se libera en el punto
. Si una partícula se libera en el punto  en el instante
en el instante  , ¿seguirá la trayectoria
, ¿seguirá la trayectoria  ;
;  ? ¿Es elíptica esta trayectoria? Justificar.
? ¿Es elíptica esta trayectoria? Justificar.

 Simulador DaVinci13- Dado el sistema
Simulador DaVinci13- Dado el sistema  . ¿Existe algún valor de
. ¿Existe algún valor de  para el cual la trayectoria de la solución es una elipse? Justificar.
para el cual la trayectoria de la solución es una elipse? Justificar.

 Simulador DaVinci
14- ¿Es posible que una partícula sometida al campo de velocidad estacionario
Simulador DaVinci
14- ¿Es posible que una partícula sometida al campo de velocidad estacionario  que
que
132
SECCIÓN IV: Teoría Cualitativa
se libera en el punto  siga la trayectoria
siga la trayectoria  ? Justificar.
? Justificar.

 Simulador DaVinci
15- Dado el sistema
Simulador DaVinci
15- Dado el sistema  ; ¿puede
; ¿puede  ser una de sus soluciones? Justificar.
ser una de sus soluciones? Justificar.

133
Ejercitación complementaria
Ejercitación complementaria
1 - Para la ecuación diferencial ordinaria de primer orden  probar que la sustitución
probar que la sustitución  la convierte en lineal de primer orden y hallar su solución.
la convierte en lineal de primer orden y hallar su solución.

2 - Probar que la sustitución  transforma la ecuación
transforma la ecuación  en una ecuación lineal de primer orden.
en una ecuación lineal de primer orden.
3 - Hallar las curvas que verifiquen  .
.

4 - Dada la ecuación diferencial  .
.
a) Determinar la solución general.
b) Determinar la curva solución que contiene al punto 

135
Ejercitación complementaria
5 - Hallar:
a) La familia de funciones que verifique la ecuación  .
.
b) La función de la familia del inciso a que cumple  .
.

6 - Determinar la solución para  cuando
cuando
 , con
, con  .
.

![]() Interactivo de Familias Ortogonales 7 - Para la familia de elipses
Interactivo de Familias Ortogonales 7 - Para la familia de elipses  , ¿son parábolas las trayectorias ortogonales? Justificar.
, ¿son parábolas las trayectorias ortogonales? Justificar.

8 - Determinar la familia de curvas solución de  . Graficar.
. Graficar.

136
Ejercitación complementaria

9 - Dada la ecuación  :
:
a) Determinar la familia de curvas solución y graficar.
b) Determinar y representar la curva de la familia que contiene al punto  y la recta tangente en dicho punto.
y la recta tangente en dicho punto.
c) Obtener una ecuación para la curva ortogonal a la familia que contiene al punto  , la recta tangente en dicho punto y graficarlas en el mismo sistema de representación del inciso b.
, la recta tangente en dicho punto y graficarlas en el mismo sistema de representación del inciso b.
137
Ejercitación complementaria


10 - La familia ortogonal a la familia  es el conjunto de elipses
es el conjunto de elipses  . Graficar dos integrantes (una de cada
. Graficar dos integrantes (una de cada
138
Ejercitación complementaria
familia) que se correspondan y sus respectivas rectas tangentes en un punto de intersección.

![]() Interactivo de Familias Ortogonales 11 - Calcular las trayectorias ortogonales a la familia de elipses
Interactivo de Familias Ortogonales 11 - Calcular las trayectorias ortogonales a la familia de elipses  . Graficar.
. Graficar.
139
Ejercitación complementaria


12 - Sea  soluciones de
soluciones de  , donde
, donde  . Demostrar que
. Demostrar que  también es solución.
también es solución.
140
Ejercitación complementaria
13 - Si  , demostrar que
, demostrar que  es solución de
es solución de  .
.
 Simulador DaVinci14 - Resolver el sistema
Simulador DaVinci14 - Resolver el sistema  ; siendo
; siendo  .
.

 Simulador DaVinci15 - Resolver el sistema
Simulador DaVinci15 - Resolver el sistema  ; siendo
; siendo  .
.

16 - Proponer las soluciones que permiten resolver la ecuación  por el método coeficientes a determinar:
por el método coeficientes a determinar:
a) 
b) 

17 - Resolver la ecuación diferencial  para:
para:
141
Ejercitación complementaria
a)  ;
;  ;
; 
b) 

18 - Dar la solución general de las siguientes ecuaciones diferenciales:
a)  ,
, 
b) 
c) 

142
Ejercitación complementaria
19- Para la ecuación diferencial  , indicar la forma de la solución propia propuesta. Expresar (sin resolver) la forma de la solución general.
, indicar la forma de la solución propia propuesta. Expresar (sin resolver) la forma de la solución general.

20- Resolver la ecuación diferencial  para:
para:
a) 

21- Dada  hallar la curva solución que pasa por el punto
hallar la curva solución que pasa por el punto  y donde
y donde  .
.

143
Ejercitación complementaria
22- Hallar la solución de la ecuación  siendo
siendo  .
.

23- Encontrar la familia de curvas solución de  que pasan por el origen de coordenadas.
que pasan por el origen de coordenadas.

24- Hallar la solución de  que cumpla
que cumpla  .
.

25- Encontrar la función  que verifique
que verifique  ,
,  e
e  .
.

144
Ejercitación complementaria
![]() Interactivo de Familias Ortogonales26- Encontrar todas las funciones
Interactivo de Familias Ortogonales26- Encontrar todas las funciones  que verifiquen
que verifiquen  e
e  . Usar el interactivo para graficar.
. Usar el interactivo para graficar.

27- Dada la ecuación  :
:
a) Proponer una solución propia para el caso en que  .
.
b) Hallar la solución general para el caso en que  .
.

28- Dado el sistema  ; dar el o los valores de
; dar el o los valores de  , si existen, para los cuales las curvas
, si existen, para los cuales las curvas que lo solucionan son elípticas.
que lo solucionan son elípticas.

145
Apéndice
Apéndice.
Fórmula exponencial de un complejo.
Recordando el desarrollo en serie de McLaurin de  ,
,  y
y  :
:

Usando estas tres fórmulas es posible obtener la forma exponencial de un complejo de la siguiente manera:
Usando el desarrollo de  se encontrará el de
se encontrará el de  :
:

147
Apéndice
Y las propiedades de la potencia de la unidad imaginaria:


Reordenando los términos de la serie es posible descomponerla en dos partes. La primera, agrupando los términos reales y la segunda, la que contiene imaginarios puros:

Sacando la unidad imaginaria como factor común de la segunda serie, puede notarse que cada una de las series involucradas son el desarrollo de  y
y  :
:
148
Apéndice

 (fórmula de Euler)
(fórmula de Euler)
Finalmente, usando las propiedades de la potencia  se llega a la forma exponencial de un complejo
se llega a la forma exponencial de un complejo  .
.

149
Apéndice
Matriz exponencial.
Usando similitud con  se define:
se define:

Usando esta definición puede mostrarse que la serie de matrices converge para todo  :
:  y
y 
Sea 
 matriz Diagonal, luego:
matriz Diagonal, luego:  .
.
 matriz de Jordan, luego:
matriz de Jordan, luego:

150
Apéndice
Si  no diagonalizable
no diagonalizable  ;
;  ;
;  y
y  .
.
151
Apéndice
Solución de sistemas de ecuaciones diferenciales lineales de primer orden. As: matriz cuadrada.
1)  es solución de
es solución de  .
.
2)  es solución de
es solución de  .
.
3)  es solución de
es solución de  .
.
4)  es solución de
es solución de  .
.
152
Apéndice
Tabla Resumen.
Solución general de sistemas lineales homogéneos 2x2 de ecuaciones diferenciales ordinarias con coeficientes constantes:


153
Epílogo
Epílogo
Las EDO abordadas en este libro son modelos simplificados de problemas que habitualmente aparecen en ingeniería. No obstante, constituyen un pequeño conjunto del vasto universo de las ecuaciones diferenciales. La mayoría de los modelos matemáticos de sistemas reales se caracterizan por su no linealidad debido a que así es el comportamiento de muchas cosas en la naturaleza. Pero para estudiar su estabilidad se recurre a su linealización, admitiendo que en este proceso se pierdan ciertas soluciones físicas. Es por ello que en la sección IV se desarrolló el concepto de estabilidad únicamente en relación a los sistemas dinámicos lineales.
Edward Lorenz, matemático y meteorólogo estadounidense, al estudiar el espacio de fases de sistemas dinámicos tridimensionales no lineales que modelan fenómenos de la atmósfera terrestre, descubrió en 1963 el llamado “atractor de Lorenz”. Con sus investigaciones sentó las bases de la Teoría del caos, rama de las matemáticas, la física y otras ciencias (biología, meteorología, economía, etc.) que trata ciertos tipos
155
Epílogo
de sistemas dinámicos muy sensibles a las variaciones en las condiciones iniciales: los sistemas caóticos. Dado que estos sistemas dependen de gran cantidad de variables, pequeñas variaciones en las mismas pueden implicar grandes diferencias en el comportamiento futuro.
Por ello Lorenz dijo que era tan difícil pronosticar las condiciones climatológicas a largo plazo. Este obstáculo de la predicción, denominado efecto mariposa (nombre devenido de la forma de mariposa del atractor descubierto), lo expuso en una conferencia bajo el título "¿Puede el batir de las alas de una mariposa en Brasil dar lugar a un tornado en Texas?".
Otros ejemplos de tales sistemas incluyen el Sistema Solar, las placas tectónicas, los fluidos en régimen turbulento y los crecimientos de población.
En la siguiente animación se muestra uno de los sistemas caóticos más simples que existen: el péndulo doble. Puede apreciarse que, además de su trayectoria irregular, depende sensiblemente de las condiciones iniciales, ya que al darle cada
156
Epílogo
vez una posición inicial ligeramente diferente, se obtiene una trayectoria completamente distinta pasado cierto tiempo.

Aquellos alumnos inquietos e interesados en asomarse al mundo de los sistemas no lineales caóticos pueden ver la película “El Efecto Mariposa”, estrenada en 2004 y que, de la mano de los directores y guionistas Eric Bress y J. Mackye Gruber, muestra cómo un ínfimo cambio en la línea del tiempo del protagonista, por más trivial o insignificante que aparente, puede provocar un rumbo totalmente inesperado y un cambio radical en su vida.
157
Epílogo
También en "El ruido de un trueno" Ray Bradbury hace una exploración a través del género literario de ciencia ficción del efecto mariposa. Cuenta la historia de un hombre que contrata los servicios de una agencia de viajes en el tiempo para participar en un safari a la prehistoria. La expedición camina sobre una plataforma de metal que gravita sobre el suelo ya que cualquier leve pisotón a un ser vivo, por pequeño que fuese, acumularía consecuencias como una gran bola de nieve hasta llegar a modificar la realidad en el presente. Para conocer el final de la historia habrá que leer el cuento, aunque se puede adelantar un detalle: el protagonista se salió de la plataforma y trajo pegada a su bota una pequeña mariposa…
Lo sorprendente es que la historia precede al trabajo de Lorenz por casi diez años, mucho antes de que fuera acuñado el término efecto mariposa y los principios entendidos por la comunidad científica. El mismo efecto ocurre en la dinámica planetaria, estudiada por Henri Poincaré hacia fines del siglo XIX, varias décadas antes de la formulación de la Teoría del caos.
La genialidad de Isaac Asimov tampoco puede dejar de
158
Epílogo
deslumbrar. En "El fin de la eternidad" presenta un mundo de viajes a través del espacio–tiempo en el que el futuro puede ser modificado; pero eso sí, bajo un meticuloso análisis que haga tender a cero la probabilidad de ocurrencia de hechos no deseados, previo a la efectiva ejecución del cambio mínimo necesario que refleje en la realidad modificada el resultado máximo esperado.
Retomando la idea de estos formidables autores del siglo XX, la serie de ciencia ficción estrenada en 2015, “El Ministerio del Tiempo”, de los directores Javier y Pablo Olivares, trata sobre una institución gubernamental secreta cuyos funcionarios vigilan las puertas de acceso hacia otras épocas para impedir que cualquier intruso viaje desde o hacia el pasado con la intención de modificar la Historia en beneficio propio. Pero los empleados de este ministerio no resisten la tentación de viajar a escondidas por asuntos personales. Por nimios que fuesen los hechos que viven cuando se transportan a todos les acarrean consecuencias... Serie digna de ver en Netflix!
159
Epílogo
Agradecimientos.
A José Román Galo Sánchez y Juan Guillermo Rivera Berrío, por su invaluable colaboración y guía en la resolución de algunos aspectos técnicos y de programación que hicieron posible este libro digital.
160
Bibliografía y Sitios Web
Bibliografía y Sitios Web.
Abreu León, J.; Oliveró Serrat, Ma.; Escamilla Gonzálex, O.; Espinosa Longi, J. (2013). Campos eléctricos en conductores. Recuperado de Red Educativa Digital Descartes: http://proyectodescartes.org/Un_100/materiales_didacticos/_Un_092_
CamposElectricosConductores/index.html. Sin fecha de publicación.
Asimov, I. (1955). El fin de la eternidad. Nueva York: Doubleday.
Bradbury, R. (1952). El ruido de un trueno. Collier's.
Emmerich, T.; Goldberg, J.; Kutcher, A. (productores) y Bress, E.; Gruber, J. (directores). (2004). El Efecto Mariposa. [cinta cinematográfica]. EU: BenderSpink, FilmEngine, Katalyst Films.
Catslash. (s.f.). Péndulo compuesto doble. Recuperado de Wikipedia: https://commons.wikimedia.org/wiki/File:Double-compound-pendulum.gif. Fecha de publicación: 22/01/2008.
Escobar Acosta, J. (2004). Ecuaciones Diferenciales con aplicaciones en Maple. Recuperado de Universidad de Antioquía - Departamento de Matemáticas:
161
Bibliografía y Sitios Web
http://matematicas.udea.edu.co/~jescobar/. Fecha de publicación: año 2004.
Olivares, J.; Olivares, P. (2015). El Ministerio del Tiempo. Serie televisiva de Netflix.
Ripoll Mira, E.; García Cebrian, M. (s.f.). Calculadora Descartes. Recuperado de Red Educativa Digital Descartes: http://proyectodescartes.org/calculadora/index.htm. Sin fecha de publicación.
Stewart, J. (1999). Cálculo multivariable. Garmendia Guerrero, D.(Traductor). México: Thomson. Tercera Edición.
Wikipedia. Teoría de la estabilidad. Recuperado de https://es.wikipedia.org/wiki/Teoría_de_la_estabilidad. Fecha de publicación: 25/01/2015.
Wikipedia. Edward Lorenz. Recuperado de https://es.wikipedia.org/wiki/Edward_Lorenz. Fecha de publicación: 24/12/2017.
162
Bibliografía y Sitios Web
Wikipedia. Teoría del caos. Recuperado de https://es.wikipedia.org/wiki/Teoría_del_caos. Fecha de publicación: 25/07/2018.
Zill, D. G. (1988), Ecuaciones diferenciales con Aplicaciones. Ojeda Peña, E. et al. (Traductores). México: Iberoamérica. Segunda Edición.
163






